FCSC, le CTF individuel de l’ANSSI
Il s’agissait des préqualifications afin de déjà écrémer les potentiels participants pour représenter la France à l’ECSC
Enormément d’épreuves étaient proposées durant ce ctf, chaque catégorie habituelle en CTF étant bien représentée. On pouvait notamment y retrouver de la crypto, du hardware (moins courant en CTF), du forensics, du reverse, du pwn, du web, de l’algo/programmation et des challs d’intro. Félicitations aux orgas et créateurs des épreuves, dont Cryptanalyse ou encore ack, alx ou sheidan qui étaient très actifs sur le serveur Discord (vous avez une liste plus complète sur leur Discord ;) ).
L’an dernier, j’avais dû arriver 10Xème, cette année j’ai essayé de tryharder beaucoup plus les épreuves et j’y ai passé beaucoup plus de temps. Je suis arrivé 29ème en sénior et 35ème en général. Pas assez pour me qualifier, mais tant pis, de base j’y croyais pas trop ^^
Au niveau de mes solves perso :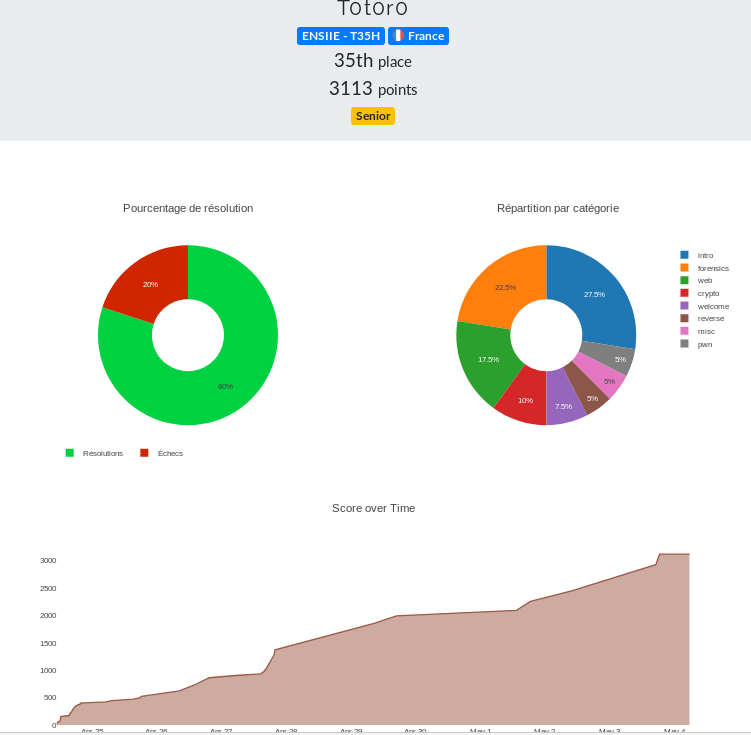
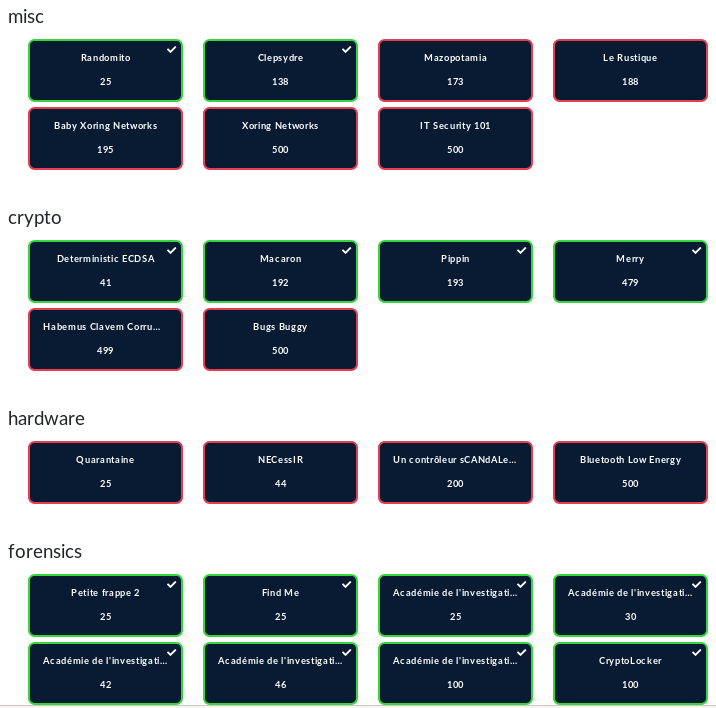
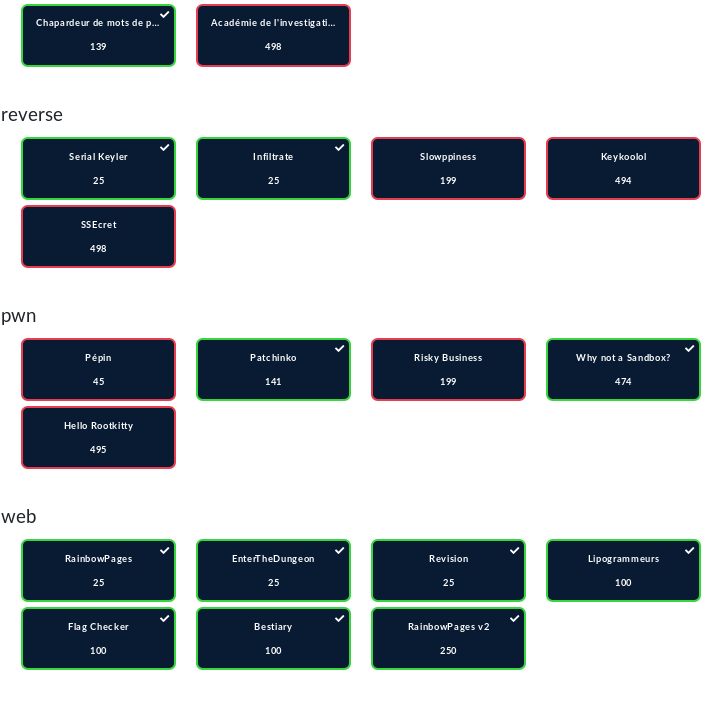

Un gros GG à :
- hexabeast le grand vainqueur en senior
- voydstack son équivalent en junior
- plus personnellement Bdenneu et Headorteil d’Hackademint
- tous les “monstres” devant moi ;p
- et à tous les participants en général ^^ (StormXploit/xbquo, Podalirius, SoEasY, Slowerzs,… et tant d'autres que j'oublie sûrement de citer ^^)
A la date et heure où j’écris cette ligne, il y a déjà eu beaucoup de writeups, j’ai donc eu beaucoup de mal à me décider sur l’intérêt ou non d’écrire tel ou tel writeup … En espérant qu’une personne trouve au moins l’un des writeups intéressant pour elle … ^^
Writeups/challenges présents ici en résumé :
- [Crypto] Macaron
- [Crypto/Prog] Merry & Pippin TODO
- [Forensic] Libreoffice TODO
- [Pwn] Why not a sandbox TODO
1. [Crypto] Macaron
Tl;dr : Signature et malléabilité grâce au XOR
Points : 192 (200 au départ)
Nombre de solves : 44
Bizarre qu’il y ait eu aussi peu de solves (genre - de solves que la pyjail “Why not a sandbox”, wtf ? o_O).
Je pense (mais je suis très mauvais pr ça xD) que la raison principale est plus le code que le problème théorique derrière … On va donc essayer de détailler un maximum pour pouvoir rendre cela clair, la plupart des WUs à ce sujet ne détaillant pas vraiment la découverte et l’analyse du code.
Enoncé :
Le but du challenge est de trouver une contrefaçon sur le code d'authentification de message Macaron.
Service : nc challenges1.france-cybersecurity-challenge.fr 2005
Nous avons en plus le code source en python du serveur :
#!/usr/bin/env python3
import os
from hashlib import sha256
import hmac
import sys
from Crypto.Util.number import long_to_bytes
from Crypto.Util.Padding import pad
from flag import flag
class Macaron():
def __init__(self, k1 = os.urandom(16), k2 = os.urandom(16)):
self.cs = 2
self.ps = 30
self.ts = 32
self.ctr = 0
self.k1 = k1
self.k2 = k2
def tag(self, input):
m = pad(input, 2 * self.ps)
nb_blocks = len(m) // self.ps
tag_hash = bytearray(self.ts)
nonce_block = long_to_bytes(self.ctr, self.cs)
prev_block = nonce_block + m[:self.ps]
tag_nonce = nonce_block
self.ctr += 1
for i in range(nb_blocks - 1):
nonce_block = long_to_bytes(self.ctr, self.cs)
next_block = nonce_block + m[self.ps*(i+1):self.ps*(i+2)]
big_block = prev_block + next_block
digest = hmac.new(self.k1, big_block, sha256).digest()
tag_hash = bytearray([x ^ y for (x,y) in zip(tag_hash, digest)])
prev_block = next_block
tag_nonce = tag_nonce + nonce_block
self.ctr += 1
tag_hash = hmac.new(self.k2, tag_hash, sha256).digest()
return tag_hash, tag_nonce
def verify(self, input, tag):
m = pad(input, 2 * self.ps)
tag_hash, tag_nonce = tag
nb_blocks_m = len(m) // self.ps
nb_blocks_nonce = len(tag_nonce) // self.cs
if nb_blocks_nonce != nb_blocks_m:
return False
if len(tag_nonce) % self.cs != 0 or len(tag_hash) % self.ts != 0:
return False
tag_hash_ = bytearray(self.ts)
prev_block = tag_nonce[:self.cs] + m[:self.ps]
for i in range(nb_blocks_m - 1):
next_block = tag_nonce[self.cs*(i+1):self.cs*(i+2)] + m[self.ps*(i+1):self.ps*(i+2)]
big_block = prev_block + next_block
digest = hmac.new(self.k1, big_block, sha256).digest()
tag_hash_ = bytearray([x ^ y for (x,y) in zip(tag_hash_, digest)])
prev_block = next_block
tag_hash_recomputed = hmac.new(self.k2, tag_hash_, sha256).digest()
return (tag_hash == tag_hash_recomputed)
def menu():
print("Commands are:")
print("|-> t tag a message")
print("|-> v verify a couple (message, tag)")
print("|-> q Quit")
if __name__ == "__main__":
L = []
macaron = Macaron()
while len(L) <= 32:
try:
menu()
cmd = input(">>> ")
if len(cmd) == 0 or cmd not in ['t', 'v', 'q']:
continue
if cmd == 'q':
break
if cmd == 't':
print("Input the message:")
message = str.encode(input(">>> "))
if not len(message):
print("Error: the message must not be empty.")
continue
tag = macaron.tag(message)
print("Tag hash: {}".format(tag[0].hex()))
print("Tag nonce: {}".format(tag[1].hex()))
L.append(message)
elif cmd == 'v':
print("Input the message to verify:")
message = str.encode(input(">>> "))
if not len(message):
print("Error: the message must not be empty.")
continue
print("Input the associated tag hash:")
tag_hash = bytearray.fromhex(input(">>> "))
print("Input the associated tag nonce:")
tag_nonce = bytearray.fromhex(input(">>> "))
check = macaron.verify(message, (tag_hash, tag_nonce))
if check:
if message not in L:
print("Congrats!! Here is the flag: {}".format(flag))
else:
print("Tag valid, but this message is not new.")
else:
print("Invalid tag. Try again")
except:
print("Error: check your input.")
continue
Initial foothold
Lisons et analysons, en restant assez haut niveau, le script python ; pour cela, on regarde d’abord le main puis les deux fonctions principales/intéressantes appelées.
Si l’on résume, nous pouvons faire 2 actions intéressantes : “tagger” un message (option t) ou bien le vérifier (option v).
Nous pouvons tagger 32 messages différents (si on en tagge plus, la variable L deviendra trop grande et on va quitter le problème) et ensuite vérifier un message ; si l’on y arrive, nous obtiendrons le flag.
-
Pour tagger, il nous suffit d’envoyer un message de notre choix, et le serveur nous retournera le tag, composé de tag_hash et tag_nonce. Le vrai tag non prévisible est tag_hash. En effet, tag_nonce dépend de self.ctr qui est incrémentée dans certaines conditions connues et de self.cs qui ne bouge pas.
-
Pour vérifier un message, il faut entrer sa valeur, ainsi que son tag ie tag_hash et tag_nonce. Ce qu’il va falloir vraiment prévoir, c’est tag_hash. On nous dira ensuite via un booléen si notre vérification est bonne ou non.
Niveau méthodo, je dirais que s’il y a une vulnérabilité, autant regarder verify : en effet, il est beaucoup plus probable qu’une vulnérabilité se trouve là-dedans au moins (il est fort probable que la vuln soit soit dans les 2 fonctions, soit dans celle-là).
Analyse rapide de verify
def verify(self, input, tag):
m = pad(input, 2 * self.ps)
tag_hash, tag_nonce = tag
nb_blocks_m = len(m) // self.ps
nb_blocks_nonce = len(tag_nonce) // self.cs
if nb_blocks_nonce != nb_blocks_m:
return False
if len(tag_nonce) % self.cs != 0 or len(tag_hash) % self.ts != 0:
return False
tag_hash_ = bytearray(self.ts)
prev_block = tag_nonce[:self.cs] + m[:self.ps]
for i in range(nb_blocks_m - 1):
next_block = tag_nonce[self.cs*(i+1):self.cs*(i+2)] + m[self.ps*(i+1):self.ps*(i+2)]
big_block = prev_block + next_block
digest = hmac.new(self.k1, big_block, sha256).digest()
tag_hash_ = bytearray([x ^ y for (x,y) in zip(tag_hash_, digest)])
prev_block = next_block
tag_hash_recomputed = hmac.new(self.k2, tag_hash_, sha256).digest()
return (tag_hash == tag_hash_recomputed)
-
Première mauvaise nouvelle, notre message m est paddé (on notera le message résultant M par la suite) :
M=pad(m,2*30)NB pour ceux qui ne savent pas ce que fait pad ici (pour les autres, vous pouvez directement aller au point suivant) :
-
Notre message est ramené automatiquement à une longueur multiple de 60. Si par exemple le message m fait 59 caractères, M sera m.\x01 où . représente l’opérateur de concaténation. Pourquoi \x01 ? Parce qu’il manque un caractère pour que le message ait une longueur voulue de 60. Si m faisait 58 caractères, on aurait eu pour M : m.\x02\x02 car nous aurions eu deux caractères manquants.
-
Si m fait strictement plus de 60 caractères, on aura la même opération, mais pour le dernier “bloc” de moins de 60 caractères de m :
Supposons que m fasse 119 chars, on peut le représenter comme m1.m2 où les mi représentent le ième bloc de 60 caractères (ou moins potentiellement pour le dernier bloc) de m. A ce moment là, on aurait M, noté M1M2 tel que M1=m1 et M2=m2.(hex(i)*i), c’est-à-dire dans notre cas m1.m2.\x01 car il manque un caractère. -
Si maintenant, la longueur de m est pile poil un multiple de 60. Bah là, on pourrait croire qu’une fonction de padding le laisserait tel quel, mais si elle faisait ça, comment est-ce qu’on pourrait différencier 2 messages a1 et a2 où a2 = a1.\x01 ? Bah on pourrait pas, car on aurait A1=a1.\x01 car il manque un caractère et A2=a2=a1.\x01 si le padding ne faisait rien. Du coup, dans ces cas-là, le padding ajoute un bloc de 60 chars, avec chaque char égal à 60 en hexa soit \x3c soit “<”.
-
Tl;dr plus “graphique” dans un interpréteur python :
>>> from Crypto.Util.Padding import pad
>>> a=“0”*59
>>> pad(a,60)
‘00000000000000000000000000000000000000000000000000000000000\x01’
>>> a=“0”*119
>>> pad(a,60)
‘00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000\x01’
>>> a=“0”*60
>>> pad(a,60) ‘000000000000000000000000000000000000000000000000000000000000<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<’
>>> ord("<")
60
>>> hex(60)
‘0x3c’ -
-
Deuxième mauvaise nouvelle :
on voit que le vrai tag qui va être calculé à partir de notre message et de notre tag_nonce (tag_hash_recomputed) est modifié dans une boucle avec un hmac utilisant une clé k1 puis qu’après cette boucle, on a encore une fois un hmac effectué avec une clé k2 différente de k1 …
L’output de la fonction tag, qui reprend exactement le même processus que celui dans verify pour le calcul du hash, ne va donc pas nous être très utile : on ne pourra pas le modifier ou en déduire quelque chose, il n’est pas malléable ; on devra donc directement utiliser la valeur exacte/identique de l’une des sorties de la fonction tag lors notre appel à la fonction verify. -
Troisième mauvaise nouvelle : pour le hmac (on utilise une fonction de hachage et un chiffrement), on utilise sha256 qui ne connaît à ce jour pas de collissions (en gros, et même si c’est imprécis, étant donné y = sha256(x), il est impossible normalement de trouver un autre x noté x’ tel que sha256(x’)=y dans des temps raisonnables)
-
Seule et unique bonne nouvelle mais de taille, on sent la vuln à plein nez : on voit un XOR, une opération avec des propriétés intéressantes :
- commutativité : a XOR b = b XOR a
- associativité : (a XOR b) XOR c = a XOR (b XOR c) et on peut donc noter cela sans ambiguité a XOR b XOR c
- a XOR a = 0 le plus intéressant
NB : ici c’est un XOR caractère par caractère, je le noterai XOR par la suite, pour le différencier du XOR habituellement rencontré en python “^”.
Dans le code, il est représenté/présent ici : [x ^ y for (x,y) in zip(tag_hash_, digest)]
On prend le 1er caractère de tag_hash, on le xor au 1er caractère de digest … bref on crée une liste l où l[i] = tag_hash_[i] ^ digest[i]
On aurait très bien pu écrire en python [tag_hash_[i] ^ digest[i] for i in range(len(digest)) ] si vous n’aimez ou ne connaissez pas zip
Analyse dans les détails de verify
Notre entrée est m, elle est paddée, ce qui nous donne M. Notre M est divisé en blocs de 30 chars.
L’entrée tag_nonce est utilisée dans la fonction pour calculer le tag final, c’est intéressant, car cela veut dire qu’il y aura peut-être un intérêt à le crafter précisément pour obtenir un tag_hash identique à un précédent. Cette entrée est également divisée en blocs mais d’une taille différente. On notera par la suite le tag_nonce N et Ni le bloc i de N.
Le tag qui va être calculé est initialisé à T0, valeur donnée et donc connue. On notera par la suite Ti le tag à l’étape i (i allant de 1 à on va dire n ; en fait la boucle va de 0 à len(nb_blocks) -1 mais ensuite on a i+1 dans les blocks du coup on peut tout décaler de 1, ça me paraît ici plus clair pour les notations).
On note H le hmac, H_k1 le hmac avec la clé k1, Hi_k1 le hmac à l’étape i
Bref, maintenant on va rentrer dans la boucle :
à chaque boucle i, on a :
big_block = prev_block . next_block = Ni-1.Mi-1 . Ni.Mi
Ti = Hi_k1 XOR Ti-1 = H_k1(big_block) XOR Ti-1 (au niveau des notations)
Si on arrive à la dernière boucle, notée n, on a :
Tn = H_k1(big_block) XOR Tn-1 = H_k1(big_block) XOR (Hn-1_k1 XOR Tn-2) en remplaçant Tn-1
De proche en proche, par une récurrence triviale, on a donc :
Tn = T0 XOR H1_k1 XOR H2_k1 XOR … XOR Hn-1_k1 XOR Hn_k1
Maintenant, imaginons qu’il est possible de crafter des Ni-1Mi-1NiMi pour qu’ils soient égaux à différentes étapes et que donc, passé à H_k1, on est des Hi_k1 égaux à différentes étapes.
Sérieux, ça serait le jackpot, ça nous simplifierait/éliminerait des opérations de boucles. et donc, si on parle et part de messages paddés avec des tailles différentes (on aura un nombre différent de blocs une fois passé ces messages dans tag ou verify), on peut peut-être avoir un même tag pour ces messages.
Pour que cela soit plus clair, prenons un exemple en faible dimension (de toute façon dans le code de l’exploit on va pas se gêner …).
Construisons/forgeons deux messages paddés avec même tag
Autrement dit, trouvons ces conditions nécessaires pour qu’une telle chose arrive
La plus petite taille d’un message (en nombre de blocs) est de base 2, la 2ème plus petite est 4, on va donc essayer de forger un message de taille 2 noté A=A0A1 et un message de taille 4 noté B=B0B1B2B3 associée tel qu’ils aient le même tag.
NB : on verra plus tard pour la forme des messages initiaux sans padding, vu qu’on sait comment padder ou virer le padding :)
On note TAi le tag à l’étape i pour le message paddé A et de même pour les TBi, HAi_k1 et HBi_k1
Pour A on a TA1 = HA1_k1 XOR TA0
Pour B, on a TB3= HB3_k1 XOR HB2_k1 XOR (HB1_k1 XOR TB0)
(pour se rapprocher ou plutôt comparer à A, on va prendre cette décomposition)
Si on se démerde pour que le début du message paddé B soit identique au début du message paddé A, on aura TA1 = TB1 (ie HA1_k1 XOR TA0 = HB1_k1 XOR TB0 pour des nonce NAi et NBi égaux ofc mais vu qu’on les contrôle, aucun problème (on les connaît dans la fonction tag et on donne les nôtres dans verify)
Donc en somme, ça serait cool que HB3_k1 XOR HB2_k1 = 0 pour arriver à nos fins
ie HB3_k1 = HB2_k1
ie HB_k1(N2B2N3B3)=HB_k1(N1B1N2B2)
ie N1B1N2B2 = N2B2N3B3
Pr cela, il faut que les chaînes de caractères soient strictement égales, ie chaque char de l’un à l’index k doit être égal au char de l’autre string au même index k et donc un slicing de l’un doit être égal au slicing de l’autre
En identifiant, on a donc :
N1=N2
B1=B2
N2=N3
B2=B3
donc en somme N1=N2=N3 et B1=B2=B3
Pour les conditions sur les débuts des messages A et B, comme dit avant, elles sont faciles à trouver :
- ils partagent le même N0 et N1, A0=B0 et A1=B1
En somme/résumé, 2 messages A=A0A1 et B=B0B1B2B3 paddés ont le même tag si :
* ils partagent les mêmes nonce (dans notre cas N0 et N1)
* A0=B0 et A1=B1=B2=B3
* N1=N2=N3
Construisons/forgeons deux messages avant padding qui auront le même tag
On l’a fait pr deux messages paddés, il suffit maintenant de construire/changer les conditions pour des messages avant padding, ce qui est assez simple et rapide :)
Pour les Ni, on on s’en fiche, on a déjà les conditions dessus :)
A doit être de longueur 2 donc le message initial non paddé doit avoir une longueur strictement inférieur à 60 :
len(a) < 60
a=a0a1
De même b = b0b1b2b3 où len(b) < 120
Pour nous simplifier la vie, on va se fixer un a pour générer un couple (a,b) ayant le même tag_hash :
On pose a=“0”*59 ie a0=“0”*30 et a1=“0”*29
On a A=“0”*59+\x01 ie A0=“0”*30 et A1=“0”*29+\x01
Maintenant, on va construire/forger b et B en déroulant les conditions :
- A0=B0 donc a0=b0
- A1=B1 ; or b1=B1 (la différence entre les Bi et bi se fera uniquement sur le dernier bloc ie b3 et B3) donc b1= A1=“0”*29+\x01
On a b0 et b1, reste à trouver b2 et b3
-
A1=B1=B2=B3
Pas de différence entre b2 et B2 donc b2=b1 -
Pour B3, on va avoir “0”*29+\x01, du coup b3 est tout simplement “0”*29
En somme/résumé, on a donc :
a="0"*59
b= b0 . b1 . b2 . b3
="0"*30 . "0"*29.\x01 . "0"*29.\x01 . "0"*29
Il suffit maintenant de coder ça, ie :
- utiliser par exemple pwntools pour pouvoir communiquer avec le serveur
- envoyer
aà tagger - récupérer le
tag_hashet letag_nonce - construire le nouveau
tag_nonceetb - envoyer le nouveau
tag_nonce,bettag_hash(qui est celui récupéré lors de l’envoi deaà la fonctiontag) à la fonctionverify
NB : Merci au writeup de StormXploit qui me permet d’avoir sans aucun effort un formalisme propre et de récupérer son script avec quelques modifications :) (parce que bon, on va pas se mentir, mon script à 1h du matin dans la nuit du dimanche au lundi, sachant que je pouvais plus participer ensuite d'ici la fin du ctf, était pas des plus clairs X) )
Script :
import os
from hashlib import sha256
import hmac
import sys
from Crypto.Util.number import long_to_bytes
from Crypto.Util.Padding import pad
from pwn import *
conn = remote('challenges1.france-cybersecurity-challenge.fr', 2005, level='error')
# Notre a d'avant, renommé mess1
mess1= b"0"*59
# On envoie a à la fonction tag
conn.recvuntil(">>> ")
conn.sendline("t")
conn.recvuntil(">>> ")
conn.sendline(mess1.decode())
# On retrieve tag_hash et tag_nonce
tag_hash=conn.recvline()
tag_nonce=conn.recvline()
tag_hash = conn.recvline()[11:-1].encode()
tag_nonce = conn.recvline()[11:-1].encode()
print(f"tag hash : {tag_hash}")
print(f"tag nonce : {tag_nonce.hex()}")
# On crée nos nonce pour notre tag_nonce
N0=tag_nonce[:4]
N1=tag_nonce[4:]
print(N0.hex())
print(N1.hex())
N2=N1
N3=N2
tag_nonce=N0+N1+N2+N3
print(f"tag nonce : {tag_nonce.hex()}")
# On crée notre b à partir de notre a, ici mess2 à partir de mess1
mess2=mess1+b"\x01"+b"0"*29+b"\x01"+b"0"*29
print("Appel à verify")
# On va envoyer b, tag_nonce et renvoyer tag_hash, récupéré de notre appel précédent à tag
print(conn.recvuntil(">>> "))
conn.sendline("v")
print("option v rentrée")
conn.recvuntil(">>> ")
conn.sendline(mess2.decode())
conn.recvuntil(">>> ")
print("mess 2 envoyé")
conn.sendline(tag_hash)
print("tag hash envoyé")
conn.recvuntil(">>> ")
conn.sendline(tag_nonce)
print("tag nonce envoyé")
print(conn.recvline())
conn.interactive()
Output et flag :
tag hash : b'e12b2320cef181c056b02dd2390e8535a396d7c00bf73c99227478935bf0ad4d'
'tag nonce : 3030303030303031'
30303030
30303031
tag nonce : 30303030303030313030303130303031
Appel à verify
b'Commands are:\n|-> t tag a message\n|-> v verify a couple (message, tag)\n|-> q Quit\n>>> '
option v rentrée
mess 2 envoyé
tag hash envoyé
tag nonce envoyé
b'Congrats!! Here is the flag: FCSC{529d5fb1ea316b2627c16190060af9f70dc420438afa7e8eb71d144a54a0}\n'
Commands are:
|-> t tag a message
|-> v verify a couple (message, tag)
|-> q Quit